It means that we can find the values of x y and z the x matrix by multiplying the inverse of the a matrix by the b matrix.
Inverse matrix method 3x3 simultaneous equations.
Enter coefficients of your system into the input fields.
1 2 3 5.
The conditions for the existence of the inverse of the coefficient matrix are the same as those for using cramer s rule that is.
Can be entered as.
Ax by h cx dy k can be solved using algebra.
All we need do is write them in matrix form calculate the inverse of the matrix of coefficients and finally perform a matrix multiplication.
What does that mean.
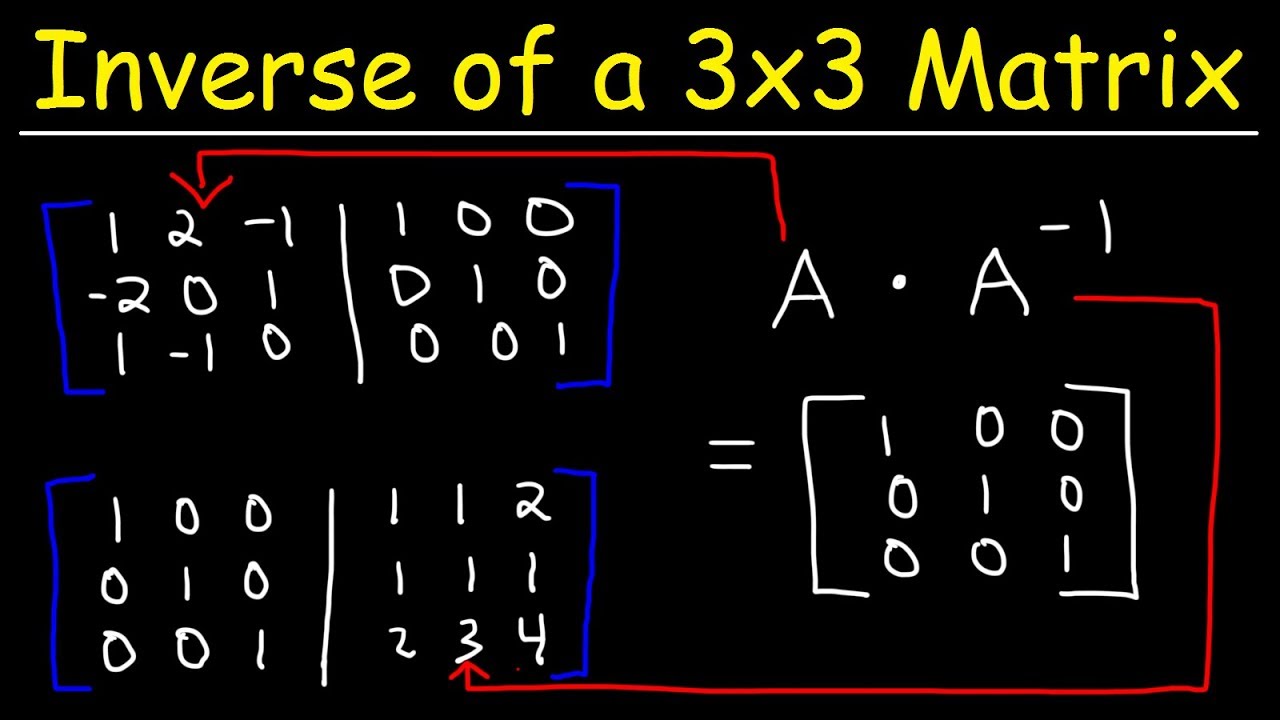
Then as shown on the inverse of a matrix page the solution is this.
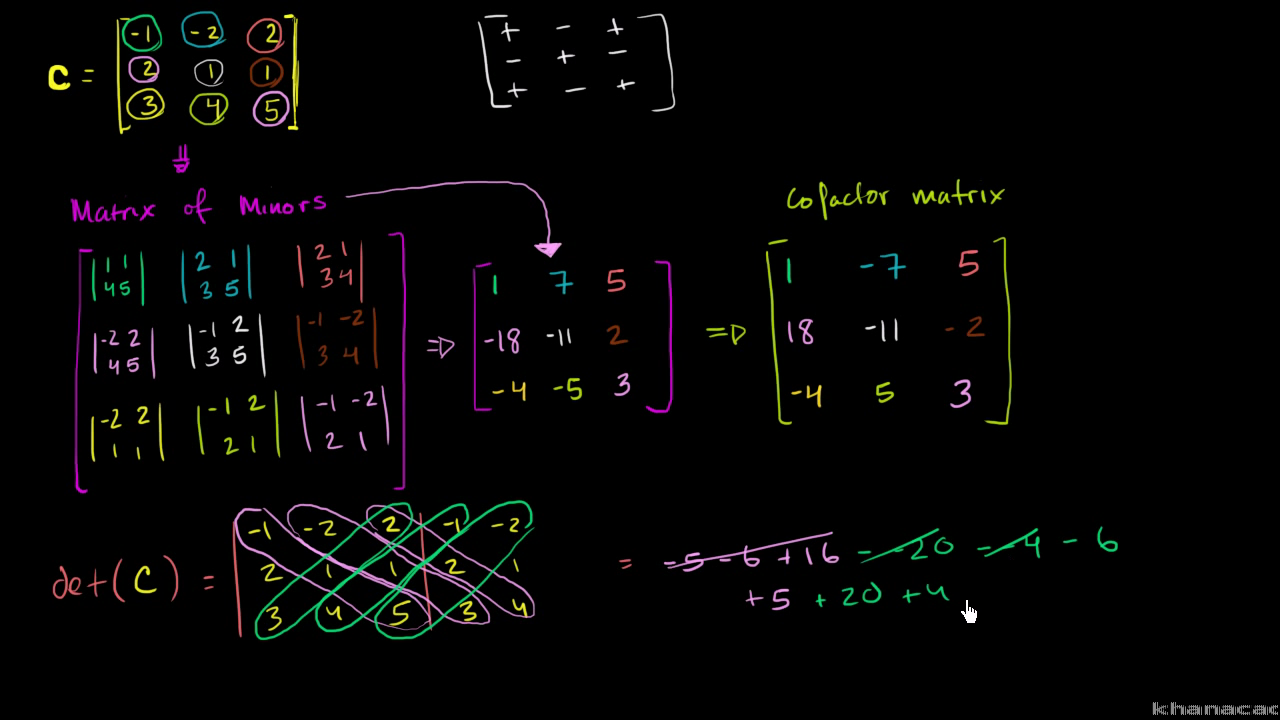
Calculating the inverse of a 3x3 matrix by hand is a tedious job but worth reviewing.
This is an inverse operation.
1 per month helps.
If before the variable in equation no number then in the appropriate field enter the number 1.
We can write this.
X 1 x 2 x 3 x 4 additional features of inverse matrix method calculator.
Similarly since there is no division operator for matrices you need to multiply by the inverse matrix.
First we would look at how the inverse of a matrix can be used to solve a matrix equation.
Write the matrix equation to represent the system then use an inverse matrix to solve it.
If in your equation a some variable is absent then in this place in the calculator enter zero.
X a 1 b.
For example the linear equation x 1 7 x 2 x 4 2.
Use a calculator 5x 2y 4x 0 2x 3y 5z 8 3x 4y 3z 11.
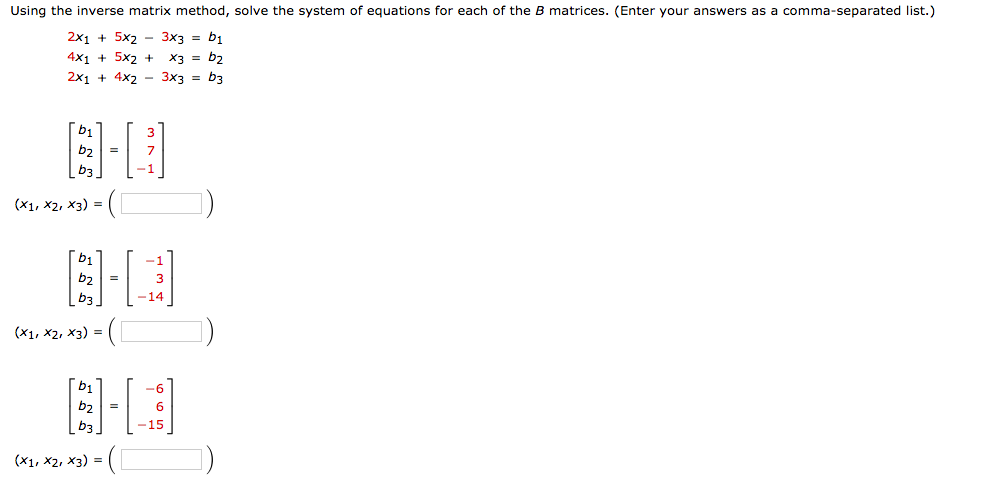
B is 6 4 and 27.
Matrix equations to solve a 3x3 system of equations example.
Thanks to all of you who support me on patreon.
How to solve matrix equations.
This calculator solves systems of linear equations using gaussian elimination method inverse matrix method or cramer s rule also you can compute a number of solutions in a system of linear equations analyse the compatibility using rouché capelli theorem.
Simultaneous equations can also be solved using matrices.
A is the 3x3 matrix of x y and z coefficients.
The determinant of the coefficient matrix must be non zero.
For example if a problem requires you to divide by a fraction you can more easily multiply by its reciprocal.
Example solve the simultaneous equations x 2y 4 3x 5y 1 solution we have already seen these equations in matrix form.
Simultaneous equations or system of equations of the form.
Given the matrix equation ay b find the matrix y.
This result gives us a method for solving simultaneous equations.
Solving a 3 x 3 system of equ.
X is x y and z and.